pySODM

Simulating and Optimising Dynamical Models in Python 3

Resources: documentation, peer-reviewed paper, pyPI

Quick installation

pip install pySODM

Aim & scope

All the simulation projects I’ve undertaken over the past six years required me to do most of the following,

1. Translate a real-world transient phenomenon into a set of differential equations called a “model” and integrate it starting from an initial condition.

2. The model’s states may be represented by n-dimensional arrays, labeled using coordinates.

3. The model’s parameters may have time-dependencies.

4. The model’s parameters may have to be sampled from distributions.

5. The model’s initial condition may have to be sampled from a distribution.

6. The model’s parameters may have to be calibrated to a dataset(s) by defining and optimising a cost function

all these features required me to wrap bookkeeping code around an ODE solver, typically scipy.solve_ivp, and I got tired of recycling the same code over and over again, so I packaged it into pySODM.

Other simulation software exists in Python, but I found most will hold your hand by having you define symbolic transitions, which places a limit on the attainable complexity of a model, making it unfit for academic research. I wanted a piece a software that nicely does all the nasty bookkeeping like keeping track of state sizes, time dependencies on parameters, aligning simulations with datasets etc. and does so in the most generically applicable way possible.

Software structure

To achieve its goal, pySODM bundles a set of low-level interfaces to integrate sets of ODEs (scipy.integrate), simulate stochastic jump processes (Gillespie methods), store n-dimensional temporal data (xarray.Dataset), perform frequentist optimizations of model parameters using Particle Swarm Optimization or the Nelder–Mead Simplex algorithm, and, perform Bayesian inference of model parameters (emcee.EnsembleSampler), all of which were already available in Python 3. pySODM adds a generic way to implement time-dependencies on model parameters, perform consecutive simulations with parameter sampling and/or initial condition sampling.

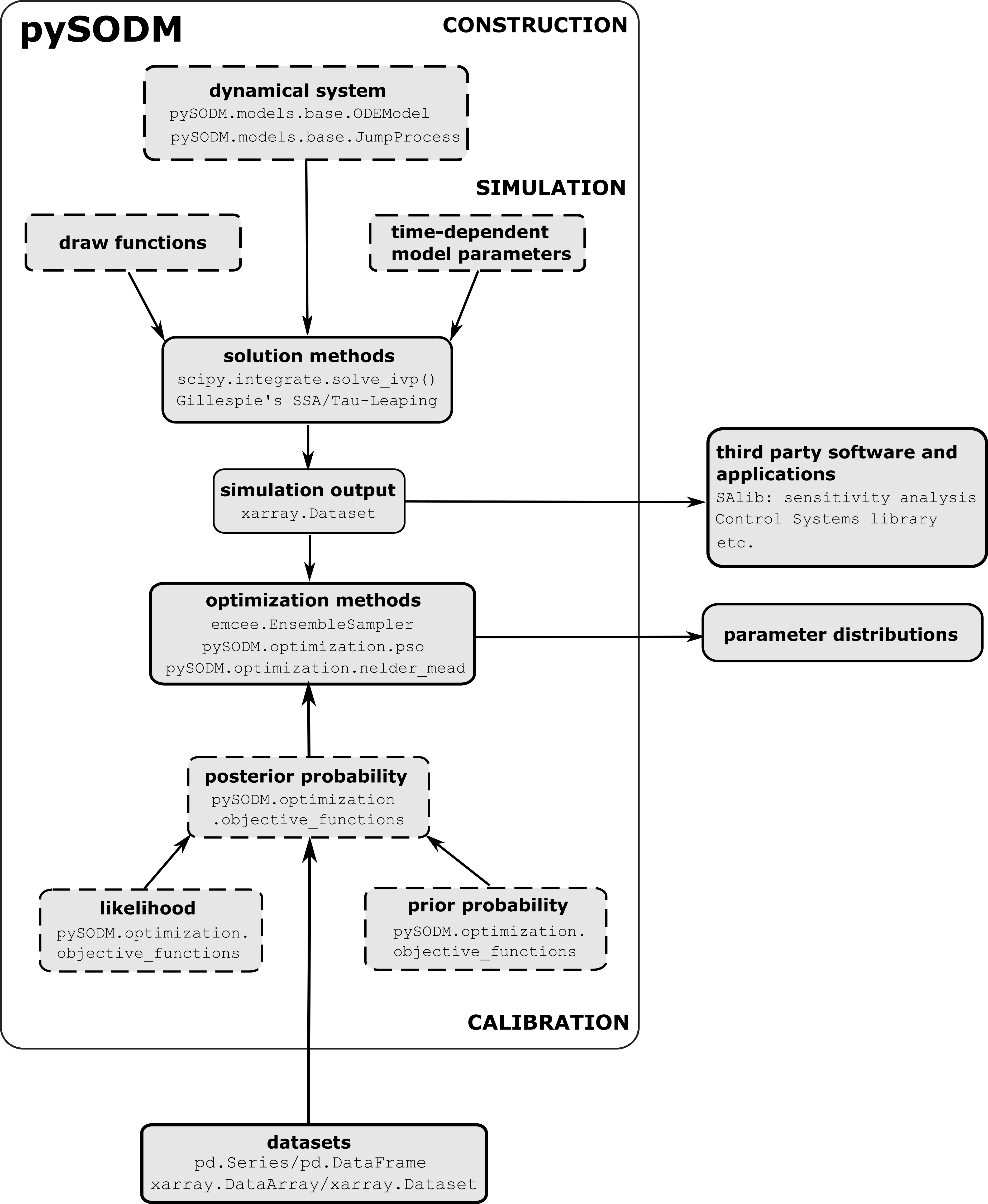
Figure Solid boxes depict third-party implementations incorporated in pySODM, while the dashed boxes depict implementations provided by pySODM.

Features

Workflow	Features
Construct a dynamical model	Implement systems of coupled differential equations
	Labeled n-dimensional model states, states can have different sizes
	Leverages xarray.Dataset to store labeled n-dimensional simulation output
Simulating the model	Deterministic (ODE) or stochastic simulation (Jump process)
	Time-dependent parameter functions to vary parameters during the course of a simulation
	Draw functions to vary model parameters during consecutive simulations
	Initial condition functions to vary the initial condition during consecutive simulations
Calibrate the model	Construct and maximize a posterior probability function
	Automatically aligns data and simulation
	Nelder-Mead Simplex and Particle Swarm Optimization
	Bayesian inference with emcee.EnsembleSampler

Getting started

• Detailed installation instructions.

• The quistart tutorial teaches the basics of building and simulating models with n-dimensional labeled states in pySODM. It demonstrates the use of time-dependent parameter functions (TDPFs) to vary model parameters over the course of a simulation and draw functions to vary model parameters during consecutive simulations.

• The workflow tutorial provides a step-by-step introduction to building a mathematical model and calibrating its parameters to a dataset. An SIR disease model is built and the basic reproduction number during an outbreak is determined by calibrating the model to the outbreak data.

• The enzyme kinetics and influenza 17-18 case studies apply the workflow to more advanced, real-world problems. In the enzyme kinetics case study, a 1D packed-bed reactor model is implemented in pySODM by reducing the PDEs to a set of coupled ODEs by using the method-of-lines. In the Influenza 17-18 case study, a stochastic, age-structured model for influenza is developped and calibrated to the Influenza incidence data reported by the Belgian Federal Institute of Public Health. These case studies mainly serve to demonstrate pySODM’s capabilities across scientific disciplines and highlight the arbitrarily complex nature of the models that can be built with pySODM. For an academic exposee of pySODM, the Enzyme Kinetics and Influenza 17-18 case studies, checkout our peer-reviewed paper.